# 回溯
回溯是一种算法思想,可由递归实现。递归是一种解决问题的方法,而回溯是一种特定的算法实现。递归是通过调用自身来解决问题的一种策略,而回溯是在解空间中进行搜索并进行选择的算法。
为什么要介绍定义?
因为之前一直将递归当成回溯,这是个错误的思想。递归的范围会更大,其囊括了回溯。
# 回溯思想
解决回溯问题,实际上就是一个决策树的遍历过程,只需要思考如下三个问题:
- 路径:就是已经做出的选择。
- 选择列表:也就是当前可以做出的选择
- 结束条件:要么满足要求,要么已经遍历结束。
框架
1 | result=[] |
在回溯算法中,撤销选择是为了回到上一步并尝试其他的选择。当我们进行回溯时,可能会发现当前的选择不满足问题的约束条件或无法得到最终的解。这时,我们需要撤销当前的选择,回到上一步进行其他的尝试。
# 经典例题
# 1 入门
# 1.1 全排列
仓库代码:全排列
力扣地址:46. 全排列
题目描述
给定一个不含重复数字的数组 nums,返回其所有可能的全排列。
1 | 输入:nums = [1,2,3] |
套用模板的代码:
1 | def permute(self,nums): |
解释
- 终止条件:根据题目要求,其返回的是全排列的所有可能结果,对于每一个结果都会包含题目所给的所有元素。因此需要选择完所有的元素再终止。
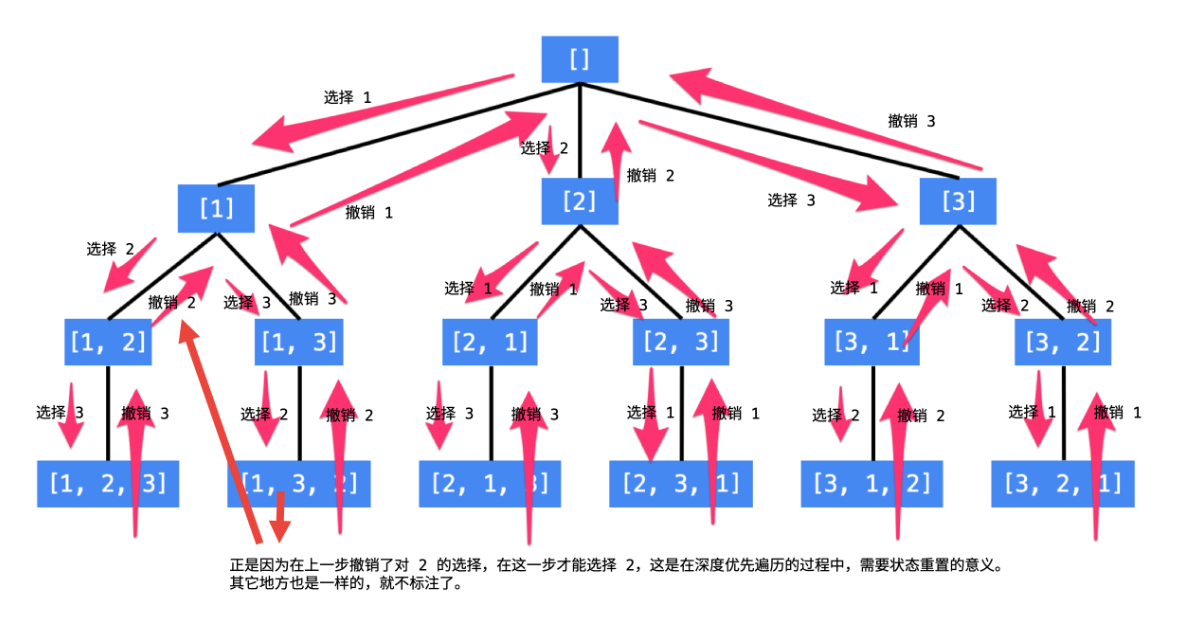
- 路径与选择
![]()
上图对应着路径与选择阶段- if 语句的作用是判断已排列的元素中是否含有当前元素,全排列是不允许已经被选择的元素再进入。而且题目要求说明了所给数字是不重复的,所以只需要判定已经参与的不再参与就行。后续会介绍所给是有重复的该如何处理。
- 进入 for 循环则进入选择阶段,对于第一个 candidate (1),先判断之前是否参与选择,如果没参与则会将 1 加入选择的列表,选择完后,再进入 backtrack 函数,进行 1 之后的元素选择【这个时候 if 判断就发挥作用了,candidate (1) 将不会被选择,而去选择剩余元素】。
- 当递归结束后,也就得到了排列为 1 开头的所有全排列。此时需要从选择里面删除 1,进入下一个 for 循环,对 2 进行搜索。
# 元素无重不可复选
# 子集
力扣地址:78. 子集
题目描述
给你一个整数数组 nums,数组中的元素互不相同 。返回该数组所有可能的子集 (幂集) 解集。不能包含重复的子集。你可以按任意顺序返回解集。
1 | 输入:nums = [1,2,3] |
题目理解
ps: 借别人的图一用,懒得画图
思路:按顺序取,只取当前元素后面的元素,即当前元素后面的元素构成候选集。
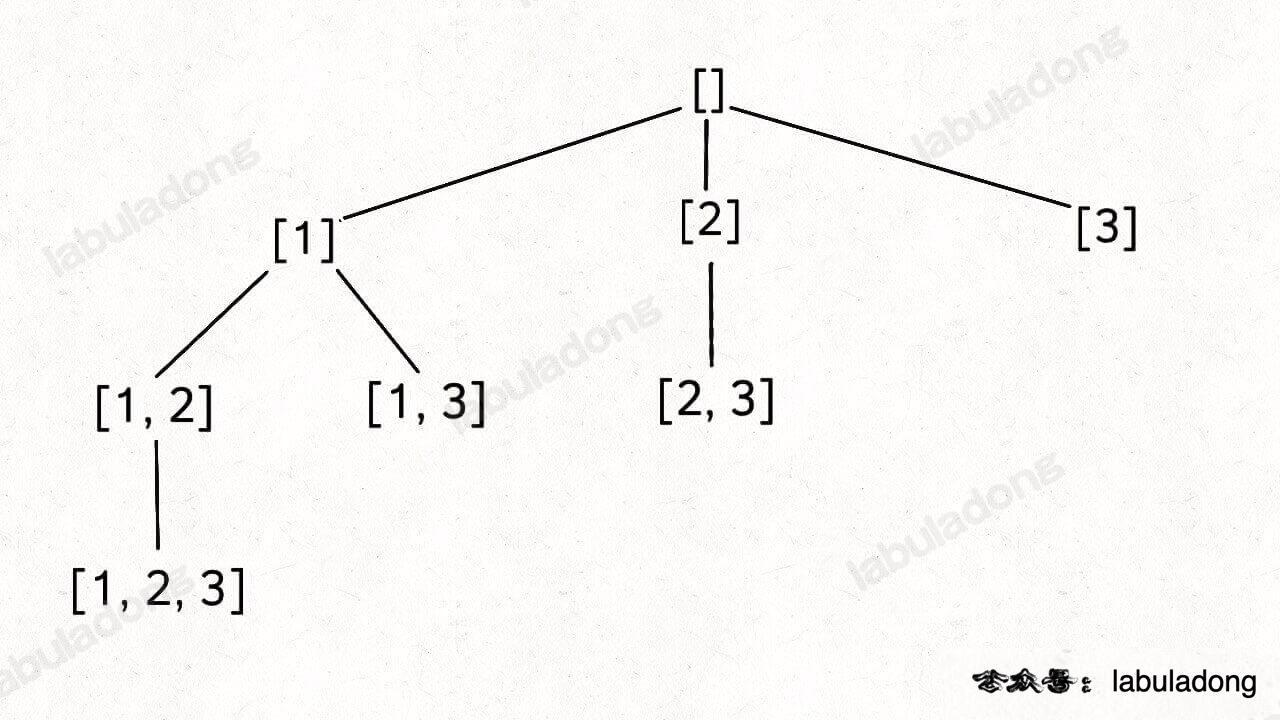
从根节点开始,题目要求是求子集,先从元素最少的子集开始,也就是空集开始,接下来是空集的子节点。在子节点做选择的时候,可选择的列表有 [1,2,3]。
- 第一个子节点,选择 1,然后进行递归,在 [1] 的基础上,生成元素为 2 的子集,这个时候能选择的列表有 [2,3]。所以能够生成两个元素个数为 2 的子集。
- 在上述生成的子节点的基础上在做选择,因此 [1,2] 可做的选择只有 [3],生成了 [1,2,3]。[1,3] 的当前元素是 3,3 后面没有新的元素,所以不产生新的子集。
![]()
因此代码上需要通过下标来遍历,让下标一直往后移动,直到循环退出
1 | class Solution(object): |
# 组合
力扣地址:77. 组合
题目描述
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。 你可以按任何顺序返回答案。
1 | 输入:n = 4, k = 2 |
题目理解
该题与子集的不同之处就在于,对子集的长度进行了要求,因此我们只需要在求子集的基础上加上长度判断即可。
核心思想依旧是将可选择列表当成有序的,只选择未被选择的元素
1 | class Solution(object): |
# 元素可重不可复选
# 子集 II
力扣地址:90. 子集 II
题目描述
给你一个整数数组 nums ,其中可能包含重复元素,请你返回该数组所有可能的子集(幂集)。 解集不能包含重复的子集。返回的解集中,子集可以按任意顺序排列。
1 | 输入:nums = [1,2,2] |
题目解释
ps:继续借图
因为有重复元素,所以首先排序,让重复元素变成相邻的元素,再对其进行预剪枝。需要结合代码理解。
- 剪枝有两个条件,
i>start and nums[i]==nums[i-1],其中i>start是保证不会删除如图所示的 [1,2] 后面的子节点 [1,2,2]。num[i]==num[i-1]是需要在前置条件满足的情况下,剪去相邻重复树枝,而不剪去子节点
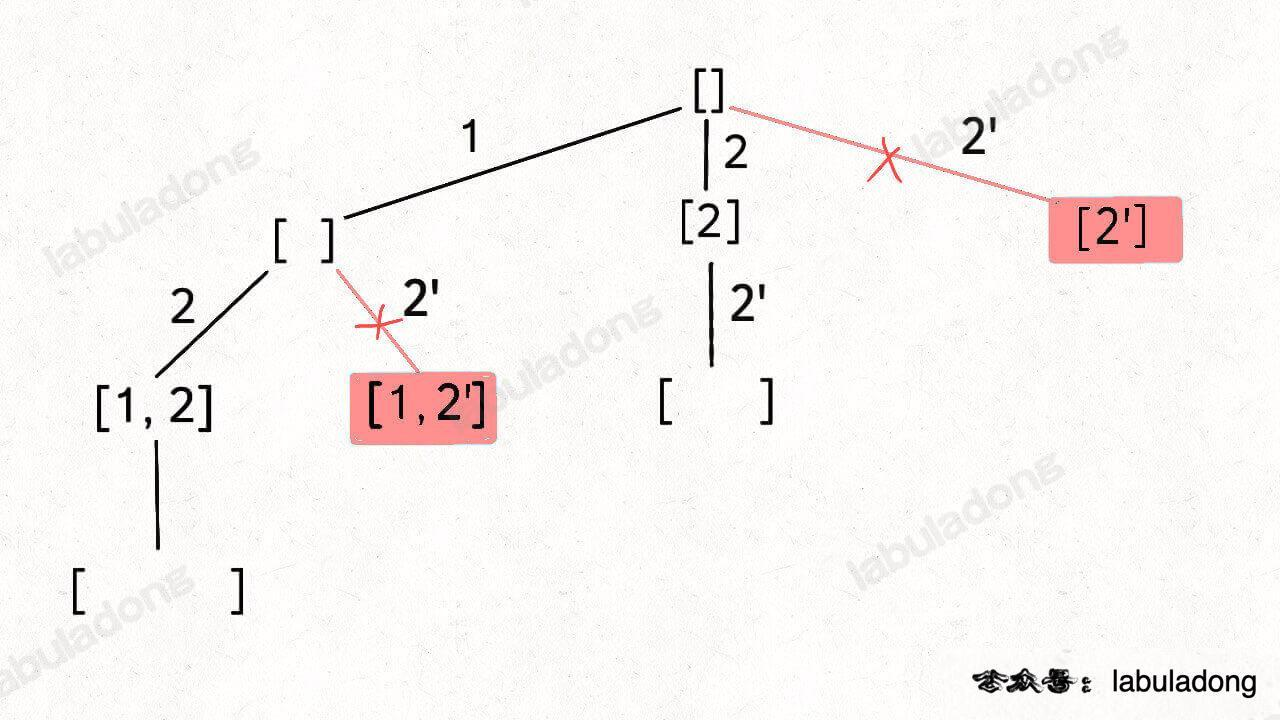
代码
1 | class Solution(object): |
# 组合总和 II
力扣地址:组合总和 II
题目描述
给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。 candidates 中的每个数字在每个组合中只能使用 一次 。
注意:解集不能包含重复的组合。
1 | 输入: candidates = [10,1,2,7,6,1,5], target = 8, |
题目解释
该题中也是包含重复元素,只需要添加一个终止条件 sum(select)==target 即可。
1 | class Solution(object): |
# 全排列 II
力扣链接:47. 全排列 II
题目描述
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
1 | 输入:nums = [1,1,2] |
题目解释
该题要求全排列、生成的结果不重复。采取的方案是全排列 + 预剪枝。后剪枝比较耗时。
1 | class Solution(object): |
为什么在递归里面需要遍历所有元素?
全排列即使你选择了中间的某个数,在接下来的递归里,仍旧有可能选择所选择的数之前的操作,所有不能使用 for i in range(start,end) ,这中 for 循环的使用形式只适用于求子集。
- 在遍历所有的元素做选择之时,有一个前提条件就是已经选择过的不能再选择。对应第一个 if 条件
if used[i]==1: - 处理重复项即剪枝,代码采用的是预剪枝的情况,如
[1,1,3],已经取了 1 用于生成第一棵递归树,此时used的第一个位置已经置为1,在进入递归时,for循环又会去遍历数组里的所有元素,但第一个1已经被用过了,则会跳过该次选择,进而去找第二个元素1,但是此时满足i>0 and nums[i]==nums[i-1] and used[i-1]==1,所以以[1,1]开头的子树将会被删除。 - 那 1,1 开头的在哪取呢:答案是以第二个
1为头节点的子树里取。这就是该代码的技巧,如果有两个元素相同,则会从第一个元素进行剪枝,而最后一个元素保留。
# 元素无重可复选
# 组合总和
力扣链接:组合总和
题目描述
给一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
示例
输入: candidates =
[2,3,5],target = 8
输出:[[2,2,2,2],[2,3,3],[3,5]]
1 | class Solution(object): |
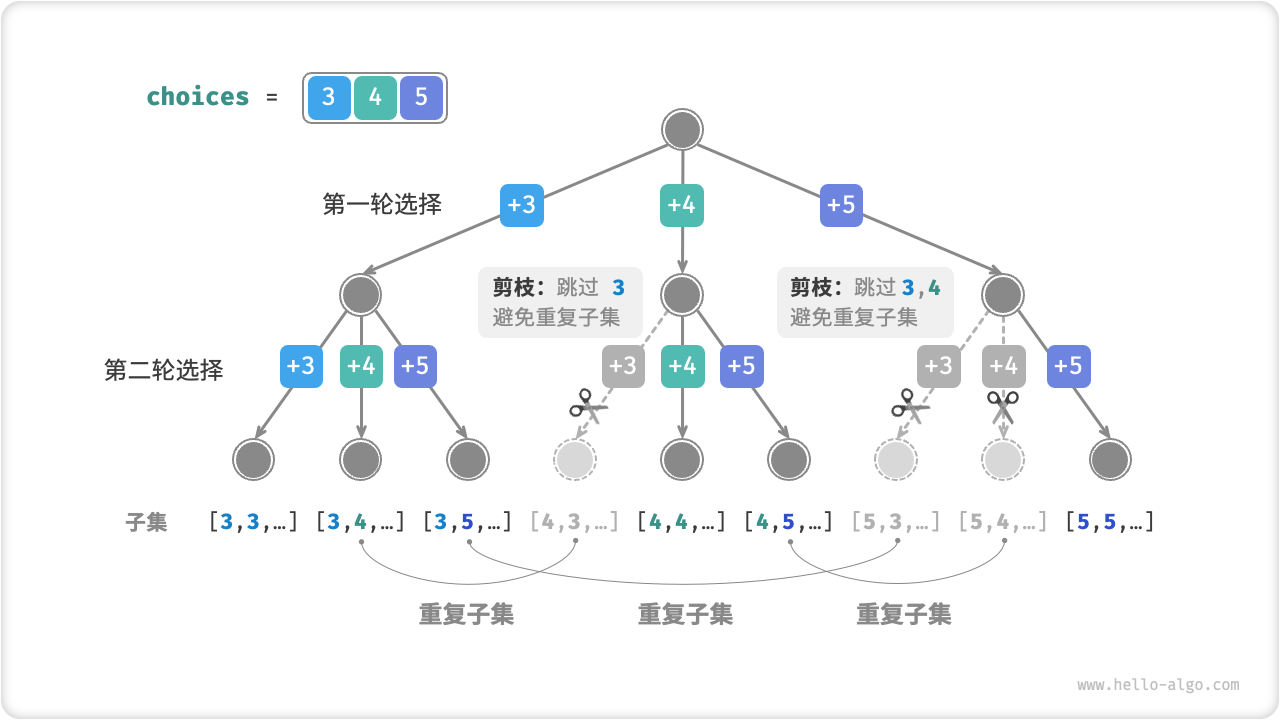
ps: 懒得画图,借图说话
思路
如果在每次递归里面都遍历所有的元素,则会造成重复,比如 [3,5],[5,3] ,这个时候可以考虑求子集的思想,遍历下标,由于题目要求可以重复选,因此每次递归时都需要包含自身但不包含自己前面的元素,以达到剪枝的目的。